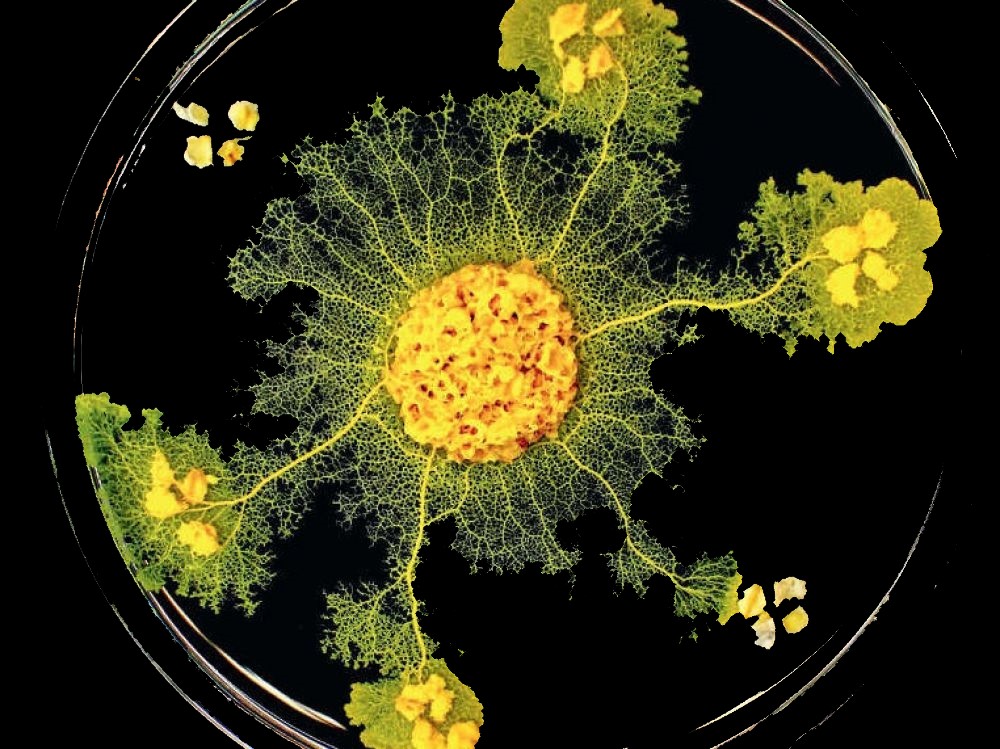


Dans la théorie du chaos, le chaos n'est pas le désordre mais l'ordre fluctuant qui s'établit entre des éléments en interaction.
Les systèmes complexes comme un écosystème, un organisme, une société, un cerveau ou l'univers sont des systèmes chaotiques dont l'équilibre est dynamique et non statique.
Lorsque l'état du système est tangent entre plusieurs évolutions possibles, des événements infinitésimaux peuvent entrainer des conséquences en chaine qui peuvent s'avérer déterminantes. C'est ce qu'on appelle "l'effet papillon", selon l'expression du météorologue Edward Lorenz (du MIT) qui a démontré que le battement d'ailes d'un papillon peut fournir l'apport d'énergie décisif qui provoquera une tornade à plusieurs milliers de kilomètres de là.


Dans un système chaotique, tout est donc une question de timing: les mêmes événements peuvent avoir des conséquences différentes selon l'état du système au moment où ils se produisent. Le plus déterminant n'est pas tant les événements eux-mêmes que leur succession dans le temps.
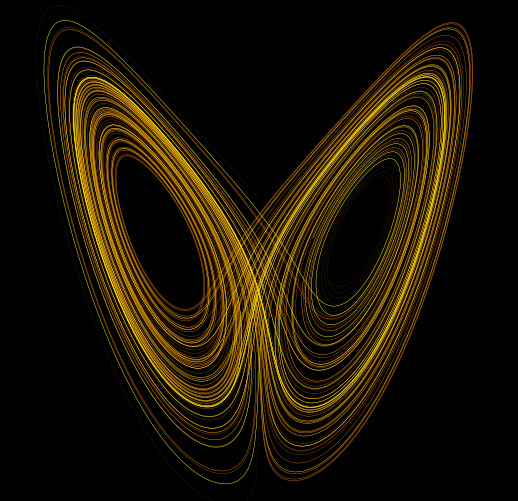
Edward Lorenz est aussi à l'origine du concept d'attracteurs.

L'attracteur étrange de Lorenz
source: http://bcev.nfrance.com/Lorenz/equations.htm
Edward Lorenz, météorologue américain au MIT, découvre en 1963 que l'on peut obtenir un comportement chaotique avec seulement trois variables, soit un système non linéaire à trois degrés de liberté. Il montre donc qu'une dynamique très complexe peut apparaître dans un système formellement très simple. L'appréhension des rapports du simple et du complexe s'en trouve profondément bouleversée. En particulier, on s'aperçoit que la complexité peut être intrinsèque à un système, alors que jusque-là on la rapportait plutôt à un caractère extrinsèque, accidentel, lié à une multitude de causes. Chez Lorenz, l'intervention de l'ordinateur est cruciale. La sensibilité aux conditions initiales, ce qu'on appellera couramment plus tard l'effet papillon , est en effet révélée par le biais de l'instabilité d'un calcul numérique. Mais, surtout, Lorenz exhibe sur son écran d'ordinateur l'image surprenante de son attracteur. Dans ses travaux de mécanique céleste, Poincaré en avait eu l'intuition, mais il l'avait évoqué par des phrases obscures : Lorenz, lui, explique sa construction par des procédures itératives et la donne à voir. Il faudra ensuite près de quinze ans pour que ces résultats soient compris et assimilés par des groupes scientifiques différents, des météorologues aux mathématiciens, des astronomes aux physiciens, aux biologistes des populations, etc.
 Les équation de Lorenz décrivent les phénomènes de convection d'un fluide idéal à deux dimensions, dans un réservoir chauffé par le bas.
Les équation de Lorenz décrivent les phénomènes de convection d'un fluide idéal à deux dimensions, dans un réservoir chauffé par le bas.dx/dt = s (y-x)
dy/dt = r x - y - xz
dz/dt = xy - b z
s, r et b sont des réels positifs. Les paramètres peuvent être interprétés de la manière suivante :
x est proportionnel à l'intensité du mouvement de convection (positif pour un mouvement dans le sens des aiguilles d'une montre, une valeur plus grande indiquant une circulation plus vigoureuse)
y est proportionnel à la différence de température entre les courants ascendants et les courants descendants (le paramètre est positif quand le fluide chaud est au fond du réservoir)
z est proportionnel à la distortion du profil du gradient de température par rapport à la linéarité (une valeur nulle correpond à un gradient linéaire, tandis qu'une valeur positive indique que la température est plus uniforme dans le milieu du réservoir, et que les plus forts gradients se trouvent sur les bords du réservoir)
t est le temps
s est la constante de Prandtl , qui caractérise la viscosité et la conductivité thermique du fluide
r est un paramètre de contrôle, qui représente la différence de température entre le bas et le haut du réservoir
b mesure le rapport entre hauteur et largeur du système de convexion
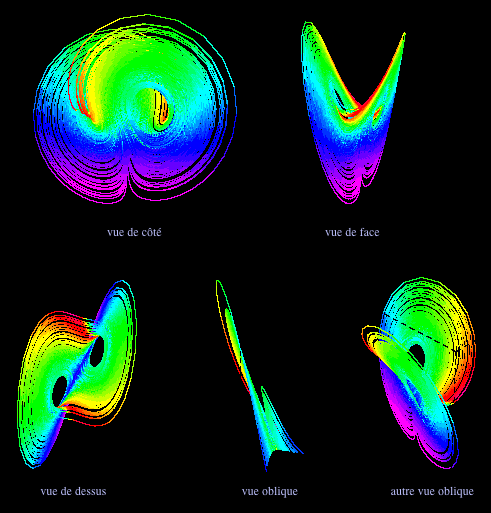
Au delà d'une valeur critique du paramètre r, le comportement du système est chaotique. L'ensemble des trajectoires possibles des phases est l'attracteur étrange de Lorenz.
Les figures ci-dessous sont des vues de l'attracteur correspondant aux paramètres : s=4 ; b=1 et r=48 (soit trois fois la valeur critique à partir de laquelle le comportement du système est chaotique)
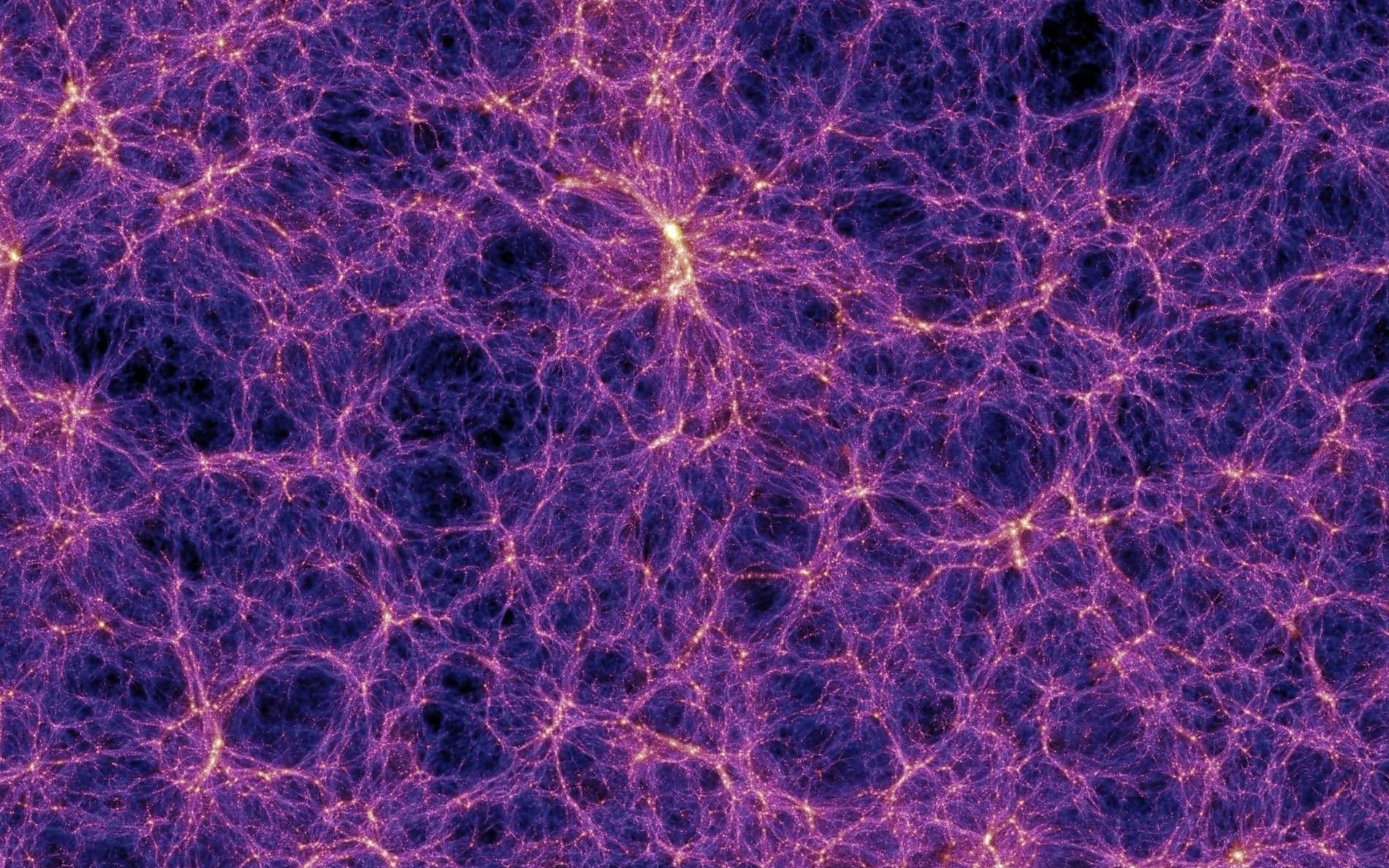
A propos de la théorie du chaos et de la prévisibilité des systèmes complexes...


"Le hasard pur n'engendre que le chaos. Le déterminisme pur ne crée rien de nouveau. C'est l'association de ces deux facteurs qui donne naissance à la richesse et à la variété des formes de la nature." Hubert Reeves
Cette interaction entre le chaos et l'harmonie semblerait être le moteur de l'évolution. Une évolution qui se veut de plus en plus riche et complexe. L'auto-organisation de la matière donne en effet à penser que l'Univers n'est pas absurde, et que son évolution à un sens, un ordre caché, qui serait présent au coeur même des phénomènes...

Par le plus grand des hasards... une gigantesque explosion, appelée communément "Big-bang", donna naissance à notre Univers. Puis, se formèrent une poignée d'atomes qui se trouvèrent par hasard quelques affinités, donnant ainsi naissance à l'eau, l'air, la terre, et la lumière. L'action combinée de ces 4 éléments donna naissance à une cellule simple qui avait reçu par hasard les "codes génétiques" nécessaires à son évolution.
Au hasard de ses mutations successives, cette cellule devint un être vivant, puis un animal, et enfin un être humain. C'est par le plus grand des hasards que cet être humain reçu en plus "la pensée" qui lui permit d'appréhender son environnement. Et c'est par hasard que cette pensée se manifestait par le biais du cerveau qui n'était qu'un assemblage savant, mais hasardeux de cellules...
L'ADN
"La vie, ce concept mystérieux, est ramenée à la présence d'ADN. Il n'y a plus de frontière entre matière animée et inanimée. Tout n'est qu'une question de degré de complexité." A. Jacquard
Le chaos et l'organisation interviennent dans la structure de l’ADN, et jouent de ce fait un rôle prépondérant dans l'évolution de la Vie. On remarquera en effet que les 3 milliards de paires de bases qui composent l'ADN, mêlées à un jeu de combinaisons entre les lettres A, T, G, et C, se trouvent elles aussi soumises aux lois du chaos...
Cela se traduit par de brusques mutations génétiques qui se veulent aussi spontanées qu'épisodiques, mais bizarrement seules les mutations ne présentant aucun frein à l’évolution, ou aucun inconvénient majeur à l'organisme seront conservées... La Vie suit alors son chemin chaotique, prenant en compte l'influence de son environnement, triant les différentes possibilités qui s'offrent à elle, évaluant et mémorisant toutes les informations soutirées, et ce afin d'offrir toujours plus de richesse et de complexité à l'évolution...
Cette interaction entre le chaos et l'harmonie semblerait être le moteur de l'évolution. Une évolution qui se veut de plus en plus riche et complexe. L'auto-organisation de la matière donne en effet à penser que l'Univers n'est pas absurde, et que son évolution à un sens, un ordre caché, qui serait présent au coeur même des phénomènes...

Par le plus grand des hasards... une gigantesque explosion, appelée communément "Big-bang", donna naissance à notre Univers. Puis, se formèrent une poignée d'atomes qui se trouvèrent par hasard quelques affinités, donnant ainsi naissance à l'eau, l'air, la terre, et la lumière. L'action combinée de ces 4 éléments donna naissance à une cellule simple qui avait reçu par hasard les "codes génétiques" nécessaires à son évolution.
Au hasard de ses mutations successives, cette cellule devint un être vivant, puis un animal, et enfin un être humain. C'est par le plus grand des hasards que cet être humain reçu en plus "la pensée" qui lui permit d'appréhender son environnement. Et c'est par hasard que cette pensée se manifestait par le biais du cerveau qui n'était qu'un assemblage savant, mais hasardeux de cellules...
L'ADN
"La vie, ce concept mystérieux, est ramenée à la présence d'ADN. Il n'y a plus de frontière entre matière animée et inanimée. Tout n'est qu'une question de degré de complexité." A. Jacquard
Le chaos et l'organisation interviennent dans la structure de l’ADN, et jouent de ce fait un rôle prépondérant dans l'évolution de la Vie. On remarquera en effet que les 3 milliards de paires de bases qui composent l'ADN, mêlées à un jeu de combinaisons entre les lettres A, T, G, et C, se trouvent elles aussi soumises aux lois du chaos...
Cela se traduit par de brusques mutations génétiques qui se veulent aussi spontanées qu'épisodiques, mais bizarrement seules les mutations ne présentant aucun frein à l’évolution, ou aucun inconvénient majeur à l'organisme seront conservées... La Vie suit alors son chemin chaotique, prenant en compte l'influence de son environnement, triant les différentes possibilités qui s'offrent à elle, évaluant et mémorisant toutes les informations soutirées, et ce afin d'offrir toujours plus de richesse et de complexité à l'évolution...

 1 commentaire
1 commentaire


 16.09.2023 - 06h34
16.09.2023 - 06h34