On doit à François Mitterrand d'importantes réalisations architecturales à Paris.

1

La première à avoir été édifiée est la Géode de La Villette, une sphère, symbole du 1, de l'unité.





2

La 2è réalisation, ce sont les colonnes de Buren, au Palais Royal. Cet ensemble est un alignement de colonnes à bandes verticales noires et blanches. Certaines sont complètement sorties du sol, d'autres à moitié, d'autres sortent à peine du sol.



Il y a "ce qui est en haut" et "ce qui est en bas"... Sous la dalle, de l'eau circule dans des canaux. La nuit, l'eau est éclairée et renvoie une leur bleutée à travers des grilles. L'eau, qui rappelle la traversée du Styx, vers l'au-delà dans la mythologie grecque. Sur l'esplanade, des balises lumineuses rouges ou vertes (selon le coté orienté vers nous) dessinent des lignes comme sur une piste d'atterrissage.




La colonne symbolise le 2, la dualité, tout comme le noir et le blanc (d'où le damier sur le sol des loges maçoniques que l'on retrouve aussi dans Matrix 1, là où Morpheus initie Neo en lui donnant la pilule rouge).


3

La 3è réalisation, c'est la pyramide du Louvre. Le triangle, symbole du 3.




4

Enfin, la 4è est la Grande Arche de La Défense. Le carré, symbole du 4.




François Mitterrand aura donc fait construire, dans l'ordre, les symboles des 4 premiers chiffres, les plus fondamentaux. Bravo l'artiste !
Le plus fort est que personne ne l'a remarqué à l'époque. On a beaucoup parlé et polémiqué à propos du coût ou de l'esthétique de ces réalisations, mais la cohérence et la portée symbolique a échappé à tout le monde en dehors des "initiés".

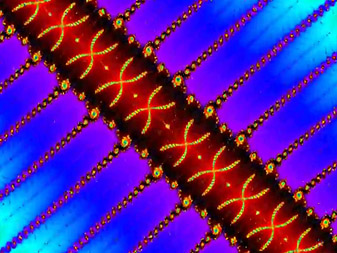
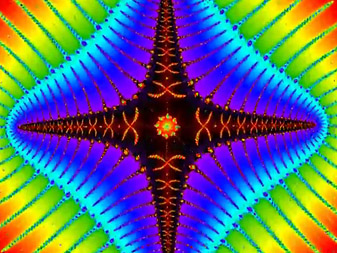
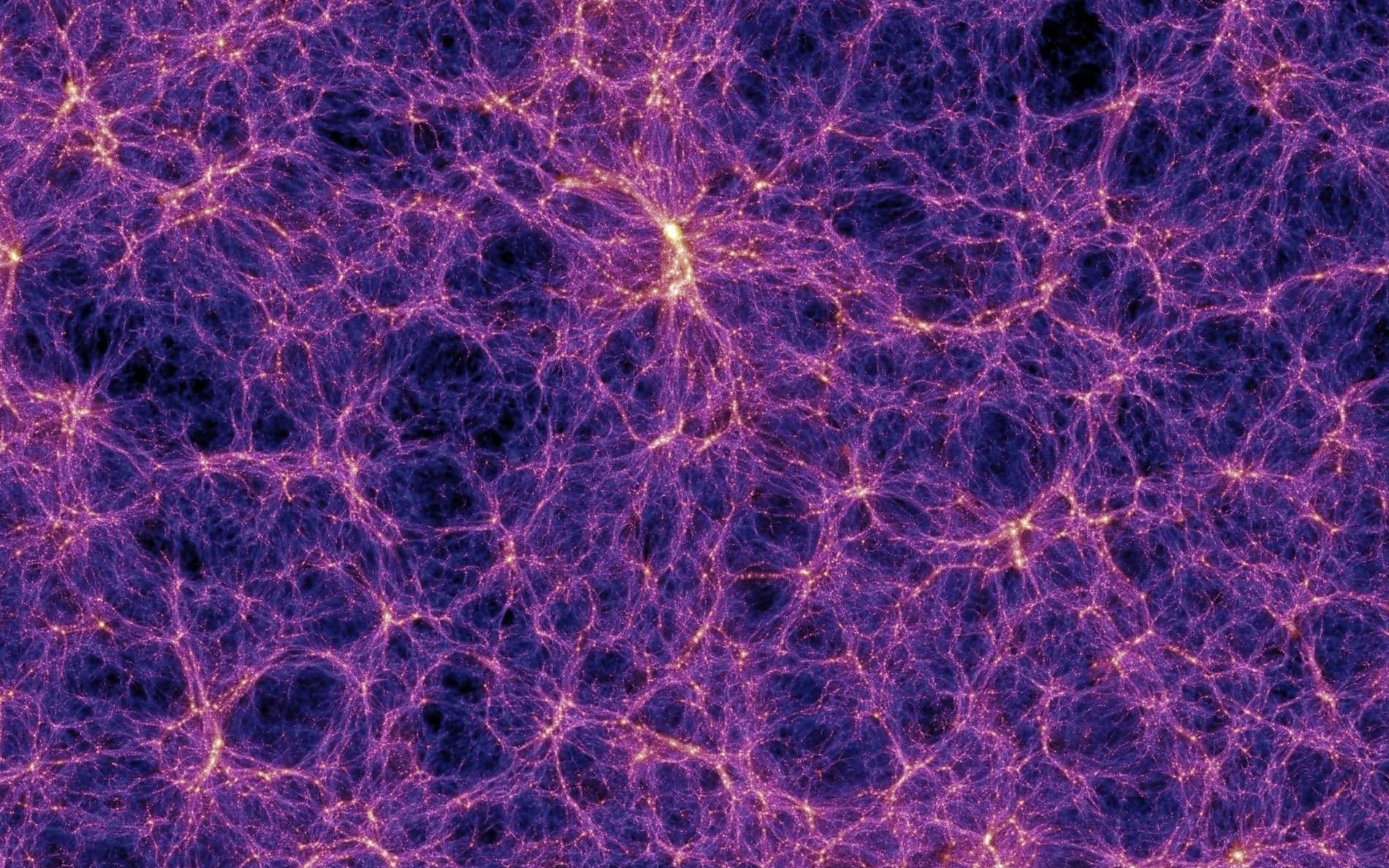
Le fractal de Mandelbrot renferme des structures étonnantes aux formes multiples qui rappellent celles que l'on trouve dans l'univers mais aussi dans le monde du vivant: spirales, coquillages, cellules, et même ce qui ressemble à des chromosomes, comme dans ce zoom profond de 10 minutes en musique... Monter le son !
 
 
 
 
 

 
 
 
 
 
Autre zoom un peu plus bref:

Un incroyable zoom de 10 minutes en continu jusqu'au plus profond du fractal de Mandelbrot...

La meilleure séquence de ce type trouvée sur YouTube et DM jusqu'à présent. Enjoy !









La même séquence en accéléré...

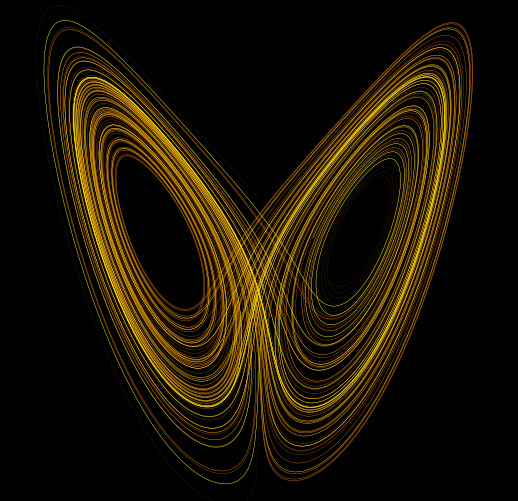
Dans la théorie du chaos, le chaos n'est pas le désordre mais l'ordre fluctuant qui s'établit entre des éléments en interaction.

Les systèmes complexes comme un écosystème, un organisme, une société, un cerveau ou l'univers sont des systèmes chaotiques dont l'équilibre est dynamique et non statique.

Lorsque l'état du système est tangent entre plusieurs évolutions possibles, des événements infinitésimaux peuvent entrainer des conséquences en chaine qui peuvent s'avérer déterminantes. C'est ce qu'on appelle "l'effet papillon", selon l'expression du météorologue Edward Lorenz (du MIT) qui a démontré que le battement d'ailes d'un papillon peut fournir l'apport d'énergie décisif qui provoquera une tornade à plusieurs milliers de kilomètres de là.






Dans un système chaotique, tout est donc une question de timing: les mêmes événements peuvent avoir des conséquences différentes selon l'état du système au moment où ils se produisent. Le plus déterminant n'est pas tant les événements eux-mêmes que leur succession dans le temps.

Edward Lorenz est aussi à l'origine du concept d'attracteurs.




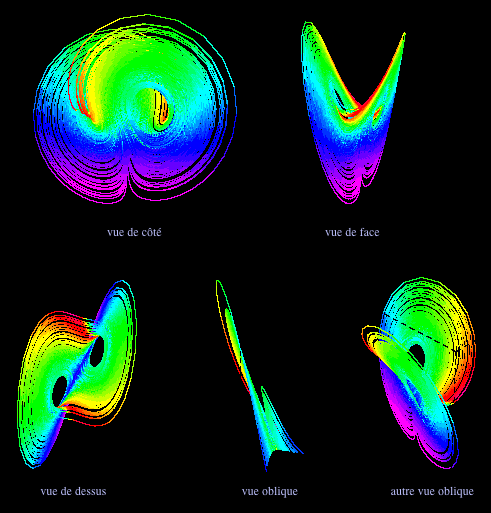
L'attracteur étrange de Lorenz
source: http://bcev.nfrance.com/Lorenz/equations.htm

Edward Lorenz, météorologue américain au MIT, découvre en 1963 que l'on peut obtenir un comportement chaotique avec seulement trois variables, soit un système non linéaire à trois degrés de liberté. Il montre donc qu'une dynamique très complexe peut apparaître dans un système formellement très simple. L'appréhension des rapports du simple et du complexe s'en trouve profondément bouleversée. En particulier, on s'aperçoit que la complexité peut être intrinsèque à un système, alors que jusque-là on la rapportait plutôt à un caractère extrinsèque, accidentel, lié à une multitude de causes. Chez Lorenz, l'intervention de l'ordinateur est cruciale. La sensibilité aux conditions initiales, ce qu'on appellera couramment plus tard l'effet papillon , est en effet révélée par le biais de l'instabilité d'un calcul numérique. Mais, surtout, Lorenz exhibe sur son écran d'ordinateur l'image surprenante de son attracteur. Dans ses travaux de mécanique céleste, Poincaré en avait eu l'intuition, mais il l'avait évoqué par des phrases obscures : Lorenz, lui, explique sa construction par des procédures itératives et la donne à voir. Il faudra ensuite près de quinze ans pour que ces résultats soient compris et assimilés par des groupes scientifiques différents, des météorologues aux mathématiciens, des astronomes aux physiciens, aux biologistes des populations, etc.

Les équation de Lorenz décrivent les phénomènes de convection d'un fluide idéal à deux dimensions, dans un réservoir chauffé par le bas.

dx/dt = s (y-x)
dy/dt = r x - y - xz
dz/dt = xy - b z

s, r et b sont des réels positifs. Les paramètres peuvent être interprétés de la manière suivante :
x est proportionnel à l'intensité du mouvement de convection (positif pour un mouvement dans le sens des aiguilles d'une montre, une valeur plus grande indiquant une circulation plus vigoureuse)
y est proportionnel à la différence de température entre les courants ascendants et les courants descendants (le paramètre est positif quand le fluide chaud est au fond du réservoir)
z est proportionnel à la distortion du profil du gradient de température par rapport à la linéarité (une valeur nulle correpond à un gradient linéaire, tandis qu'une valeur positive indique que la température est plus uniforme dans le milieu du réservoir, et que les plus forts gradients se trouvent sur les bords du réservoir)
t est le temps
s est la constante de Prandtl , qui caractérise la viscosité et la conductivité thermique du fluide
r est un paramètre de contrôle, qui représente la différence de température entre le bas et le haut du réservoir
b mesure le rapport entre hauteur et largeur du système de convexion

Au delà d'une valeur critique du paramètre r, le comportement du système est chaotique. L'ensemble des trajectoires possibles des phases est l'attracteur étrange de Lorenz.

Les figures ci-dessous sont des vues de l'attracteur correspondant aux paramètres : s=4 ; b=1 et r=48 (soit trois fois la valeur critique à partir de laquelle le comportement du système est chaotique)





A propos de la théorie du chaos et de la prévisibilité des systèmes complexes...